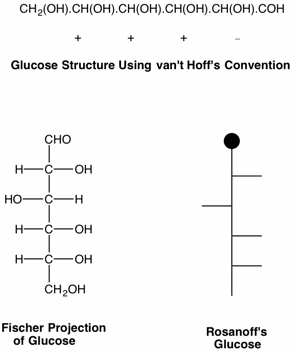
Every scientific discipline has a history and every history has landmark events of intellectual brilliance. What Darwin was to evolution, what Newton and Einstein were to physics, we may add the name of Emil Fischer and his contribution to organic chemistry - the determination of the structure of glucose in 1891. This remarkable example of intellectual prowess required factual information about the sugars that were known at the time, great patience in handling substances that were difficult to purify, but as important, what was required was a paradigm with which to unravel the disparate data available on the sugars. This paradigm was recognized by Fischer as the tetrahedral, asymmetric carbon, put forth by van't Hoff in his 1874 pamphlet, "The Arrangement of Atoms in Space". Fischer's "Proof" using the notation of van't Hoff is somewhat difficult to follow. For this reason, Fischer quickly followed his original paper with one that introduced what we now refer to as the Fischer projections. Rosanoff further streamlined Fischer's projection in 1906.

Before we set out on this
adventure, some background on the status of carbohydrate chemistry in
1884, when Fischer began his research in this area, is warranted. The
analytical tools that were available to him were combustion analysis,
melting point, optical rotation and reason. The known monosaccharides
included (+)-glucose (dextrose; from its sign of rotation),
(+)-galactose, (-)-fructose (levulose; from its sign of rotation),
and (+)-arabinose. In the late 1880's, Heinrich
Kiliani developed the chain extension method using hydrogen cyanide
to form aldonic (glyconic) acids containing an additional carbon
atom. The reduction of these polyhydroxylated carboxylic acids with
red phosphorus and HI afforded alkanoic acids. Using these techniques
arabinose was shown to be an aldopentose in that it produced n-hexanoic
acid. Glucose was shown to be an aldohexose (n-heptanoic acid) while
fructose, through the formation of 2-methylhexanoic acid, was
formulated as a 2-ketohexose. Fischer was able to prepare a new
aldohexose, (+)-mannose, from (+)-glucose.
Early in Fischer's career (1875), at the age 23, he published a paper on the formation of phenylhydrazine by the reduction of
phenyldiazonium nitrate with potassium bisulfite. Ironically, this substance was to prove
critical in the elucidation of the structure of glucose and its
isomers. In the preparation of (+)-mannose from (+)-glucose, Fischer
realized that these two aldohexoses were epimeric at C2.
This was true of the respective aldonic acids, gluconic and mannonic
acids wherein the aldehyde group had been oxidized to a carboxylic
acid group. In fact, upon heating either of these acids in the
presence of the base quinoline, a mixture of gluconic acid and
mannonic acid was produced. Furthermore, the two monosaccharides
formed different phenylhydrazone derivatives but they formed the same
osazone, which were identical to the osazone formed from
(-)-fructose. The process of osazone formation is an oxidation that
destroys the stereochemistry at C2, forming a phenylhydrazone at C1 and C2. In addition, reduction
of (-)-fructose with sodium amalgam afforded both glucitol (sorbitol)
and mannitol. Thus, the absolute configuration at C3,
C4, and C5 must be the same in all three
monosaccharides.
Following the lead of
van't Hoff, Fischer
realized that (+)-glucose had to be one of the 16 possible structures
shown in Scheme 1. Thus, 1 is the enantiomer of 9, 2 the enantiomer
10, ...etc. If one of the structures 1- 8 is (+)-glucose, then its
enantiomer, (-)-glucose is n + 8, or visa versa. Because the pairs,
1/2, 3/4, 5/6, 7/8 ...etc. are epimeric at C2, if one of
them is (+)-glucose, then the other one must be
(+)-mannose.
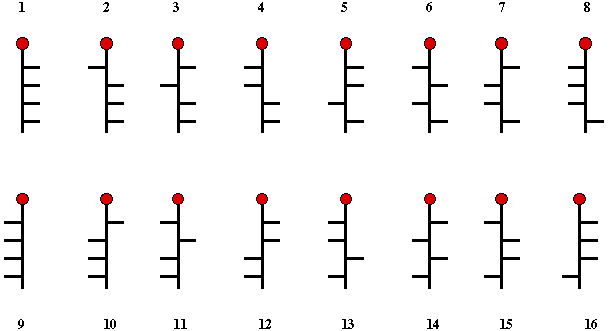
Scheme 1
Fischer reduced the number of
possibilities for the structure of (+)-glucose by considering the
optical properties of derivatives of glucose that had the same
achiral groups at C1 and C6, namely glucaric
acid [C1 = C6 = CO2H, an aldaric
(glycaric or saccharic) acid] as well as the hexahydroxy alcohol,
glucitol [sorbitol, an alditol (glycitol)]. Both glucaric acid and
glucitol are optically active. Thus structure 1 is the same as 9 and
7 is the same as 15. They are meso compounds and optically inactive.
None of them is related to (+)-glucose.
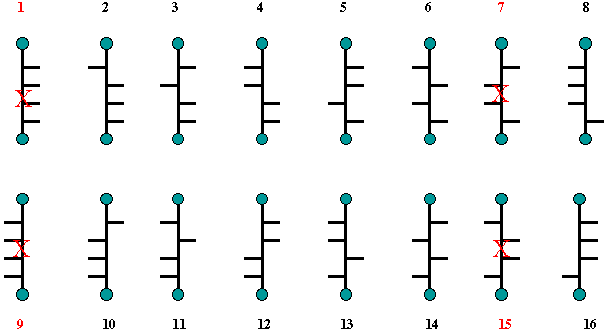
Scheme
2
Now, mannaric acid, as well
as mannitol, is optically active. If structure 8 (or its enantiomer
16) in Scheme 2 were glucaric acid (or glucitol), then structure 7
(=15) would have to be mannaric acid. But structure 7 is optically
inactive. Therefore, structures 8 and 16 cannot represent glucaric
acid in Scheme 2 nor can structures 8 and 16 in Scheme 1 represent
(+)-glucose. For the same reason, Structures 2 and 10 in Scheme 2
cannot represent glucaric acid or glucitol because structure 1 is
optically inactive and it cannot represent mannaric acid or mannitol.
Fischer was half way home; he was now left with the options presented
by Scheme 3.
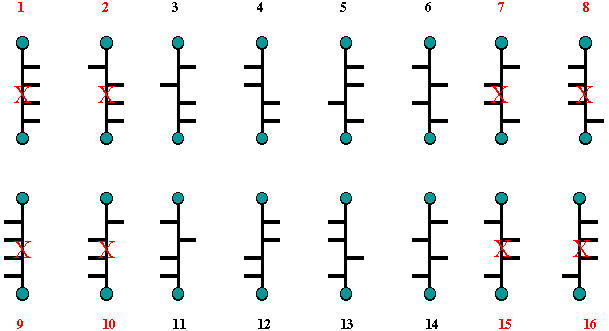
Scheme 3
Chain extension
through the Kiliani procedure was now going to play a key role. The
pentose (+)-arabinose from beet pulp gave two aldonic acids: gluconic
acid and mannonic acid, both of which were enantiomers of the aldonic
acids obtained previously. From these new enantiomers were prepared
both (-)-glucose and (-)-mannose. The implications were clear. The
relative configuration at C3, C4, and
C5 in (+)-glucose and (+)-mannose must be the same as the
respective carbons C2, C3, and, C4
in (+)-arabinose but opposite in the absolute sense. Here was a
seemingly simpler problem; determine the structure of arabinose. In
Scheme 4 are the 8 remaining options for the structure of (+)-glucose
along with the 4 possible structures for (+)-arabinose. The pentose
structures are situated between the two hexoses they form on chain
extension. Note that the newly introduced hydroxyl groups are
designated in
red,
and A and A' are enantiomers as are B and B'.
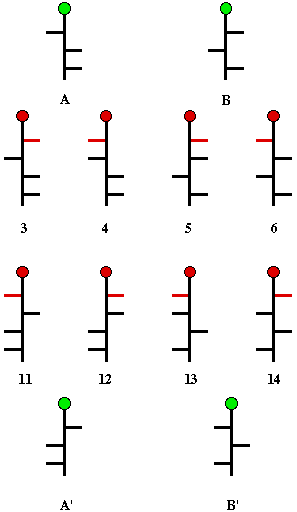
Scheme 4
Fischer again called upon symmetrization. Oxidation
of C1 and
C5
of (+)-arabinose gave an optically active trihydroxyglutaric acid,
arabinaric acid (Scheme 4). Similarly, reduction of (+)-arabinose
afforded a seemingly optically inactive arabitol. These apparent
conflicting observations were too important to ignore. Realizing that
borax complexes of optically active polyols give enhanced rotations,
Fischer applied this technique to arabitol; optical rotation was
observed. From these data Fischer was able to conclude that the
enantiomers of arabinose are represented by the structures A and A',
and that glucose must be among the structures 3 and 11, or 4 and 12.
Clearly, symmetrization of B or B' would lead to optically inactive
products. Whichever pair represented the enantiomers of glucose, the
other pair had to represent the enantiomers of mannose.
Fortunately for Fischer, a new pentose,
(+)-xylose, had been discovered in 1886. Upon subjecting (+)-xylose
to the symmetrization processes conducted on arabinose, both the
xylaric acid and the borax complex of xylitol were shown to be
optically inactive. There are only four structures that are
candidates for (+)-xylose: B, B' (Scheme 4), and the pair of pentoses
having the hydroxyl groups at the three asymmetric carbons all on one
side of the Fischer projection. When the Kiliani chain extension was
applied to (+)-xylose, a new levorotatory aldonic acid was isolated.
Oxidation of this substance with HNO3 provided a
trihydroxyglutaric acid, which was recognized by Fischer as the
enantiomer of the glucaric acid derived from (+)-glucose. This new
hexose was, therefore, (+)-glucose with the C1 and
C6 groups switched. Because of this structural
relationship, Fischer switched the "l" and the "u" in glucose and
dropped the "c" to dub the new hexose, (-)-gulose. Indeed, Fischer
was able, through a number of chemical transformations, to switch the
head (C1) and the tail (C6) of (+)-glucose to form the enantiomer of
(-)-gulose, (+)-gulose.
Now it was clear which structures of Scheme 4 represented glucose and
which one is mannose. Only structures 3 and its enantiomer 11 can be
glucose because only this pair can form the same aldaric acid from
another hexose, namely gulose. The enantiomers of gulose must be
structures 5 and 13. Mannose (4 and 12) are the only hexoses that can
form mannaric acid because of its internal two-fold axis of symmetry.
Fischer had no way to determine whether (+)-glucose was represented
by structure 3 or 11. So, he made a guess. He assigned structure 3 to
(+)-glucose and defined it as a member of the d-series. Fischer's
guess eventually was shown to be correct. Obviously, (-)-glucose
would be a member of the l-series.
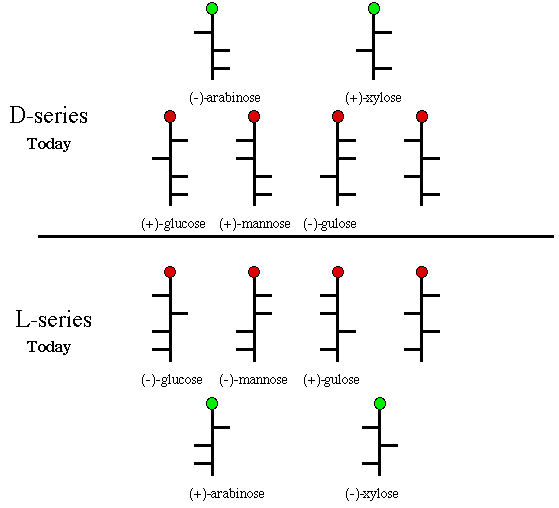
[Note: Today we use the terms d- and l- as descriptors for optical rotation, the equivalent of + and -, respectively. In Fischer's day lower case letters were used to designate configuration. Today we employ upper case letters. Any carbohydrate that can be chemically, or biochemically, related to (+)-glucose was also considered a member of the d-series. While the structure of glucose and its isomers was on solid ground, the d/l-series designation was to lead to confusion. For instance, it did not preclude two enantiomeric carbohydrates being converted into (+)-glucose. Would both enantiomers be members of the d-series? These lower case letters were raised to upper case, D- and L-, retaining Fischer's meaning, but they did not have the same meaning as the D- and L- descriptors we use today. Fischer considered (+)-glucose and (+)-gulose as members of the D-series because the formed the same enantiomeric aldaric acid, glucaric acid. It is clear from Scheme 5 that these two aldohexoses are not in the same series. Today we use the following formulation. Any monosaccharide having the hydroxyl at the highest numbered asymmetric carbon on the righthand side of the Fischer projection (drawn as they are in Scheme 5) is a member of the D-series. Those sugars with the hydroxy on the left at the same carbon are members of the L-series. The six monosaccharides on the top of the diagram in Scheme 5 are D-sugars; the six on the bottom are L-sugars. For a discussion of the evolution of the modern usage of D- and L-series, consult the work of M. A. Rosanoff.]
copyrighted F. E. Ziegler 2002