Emil Fischer's determination of the relative stereochemistry of (+)-glucose in 1891 and his lucky choice of which enantiomer represented (+)-glucose stands as a landmark achievement in organic chemistry. This accomplishment put the asymmetric carbon, as championed by van't Hoff and LeBel, on a firm footing from which there was no retreat.

Figure 1

Fischer also focused on classifying the aldoses (monosaccharides) into two families: the d-series and the l-series. The d-series was that group of compounds that could be related to (+)-glucose [Fig. 1] chemically while the l-series was related to (-)-glucose. Thus, (+)-gulose is in the d-series because it and (+)-glucose form the same enantiomeric aldaric (glycaric or saccharic) acid. In a 1906 paper, M. A. Rosanoff took issue with this argument of Fischer. Rosanoff formulated Fischer's position as follows:

"Two aldoses can produce the same dibasic acid only if they belong to the same stereochemical family. That this, however, is erroneous as a general proposition, may be readily seen from the fact that the two enantiomorphous galactoses - plainly belong to the opposite families - yield the same mucic acid." [Fig. 2]


Figure 2

Fischer's scheme must assume that two enantiomeric aldoses cannot form the same glucose enantiomer. That is, there is the implicit assumption that the two families or series are mutually exclusive. Rosanoff proposed a classification that was ultimately based on the Kiliani homologation and Ruff/Wohl degradation of aldoses. He named these two series using Greek descriptors as the δ-family and the λ-family to distinguish them from Fischer's d- and l-families. In the ensuing discussion, Fischer's d and l appear in upper case as D and L. Although the Rosanoff scheme would survive, it did so by replacing the Greek descriptors with D and L as we understand them today.

In the circular chart by Rosanoff shown below, the vertical axis separates the λ-series (left side) from the δ-series (right side). The λ-series contains four D-aldoses [Fischer designation] while their four mirror image L-aldoses are contained in the δ-series. In the center of the diagram is the two carbon, achiral compound, hydroxyacetaldehyde (HOCH₂CHO). Every successive circle homologates the central structure by -CH(OH)-, that is, a Kiliani synthesis. The number of structures in each shell doubles by 2^n-1 where the innermost circle is n=1. The outermost circle ( n=5) bears the 16 aldohexoses. The aldoses in each successive circle, proceeding outward, are the C₂-epimers derived from the aldose in the inner circle with which they are contiguous.

If the vertical north-south axis is treated as a mirror, every structure on the left is the mirror image of the one on the right. All of the structures on the left have the highest numbered asymmetric center (most remote from the aldehyde group) on the left of the Fischer projection. The converse is true on the right. It is apparent from the Rosanoff scheme that (+)-glucose (10) is in the δ-family while (+)-gulose (12) is in the λ-family. As noted earlier, the Fischer designations of D and L were dropped and Rosanoff's δ became the new D while λ became L. The left side of the diagram is referred to as the L-series; the right side as the D-series.
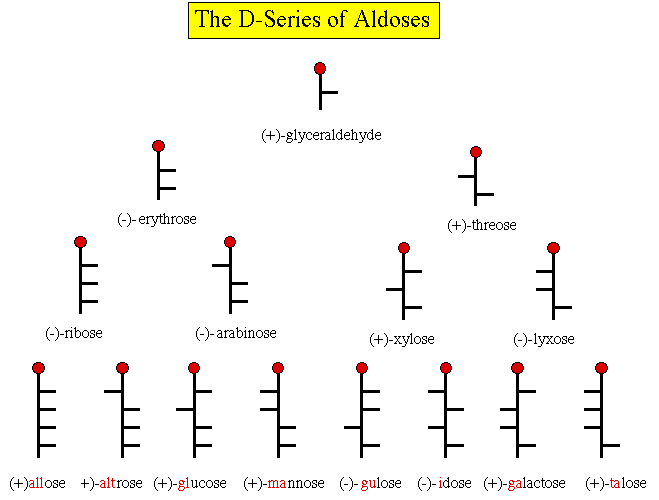
The right side of Rosanoff's circular diagram is usually presented today as a pyramid shown below. A mirror image pyramid can be constructed for the left side of the diagram as well. Starting with glyceraldehyde, Kiliani synthesis gives the aldotetroses, erythrose and threose. Similarly, the tetroses afford the aldopentoses, which lead to the aldohexoses. The nonsense line, "All altruists gladly make gum in gallon tanks" , is a mnemonic to help remember the names of the aldohexoses. [Fieser & Fieser, Advanced Organic Chemistry, 1965, pg. 947]. How about a devise for the 7 aldoses at the top of the chart? Here is a start; GET Rest At Xanadu Lodge. OK, how about GET Rems at X-ray Lab. You're on your own!

copyrighted F.E. Ziegler 2002