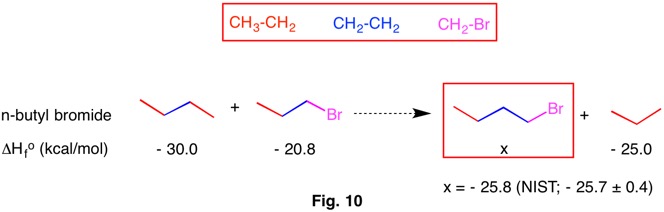
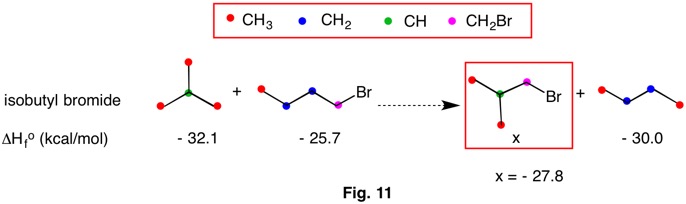
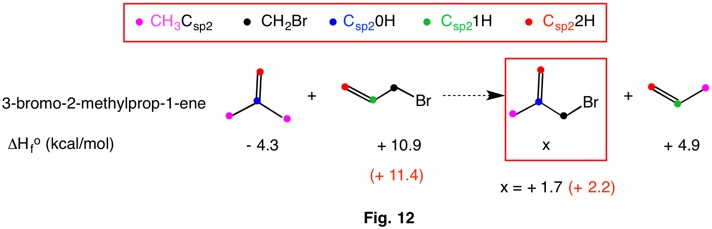
In 2009 Wheeler, Houk, Schleyer and Allen codified and redefined bond separation reactions into a heirarchy of reaction conditions (RC). Bond separation reactions are conceptual and hypothetical, and need not be able to be executed in a laboratory. The higher the RC ranking, the more dependable the method is for determining thermochemical data by computational methods. The chart below reveals that each RC-n is a subset of the ones to its right. That is, RC-5 is a subset of RC-4 and RC-4 is a subset of RC-3, etc. As one moves from RC-1 (isogyric) to RC-5 (hyperhomodesmotic), the conditions for classification become more restrictive and more effective at predicting thermochemical data. The desmotic reactions (RC-3, RC-4, RC-5) that do not involve resonance stabilization or ring strain have heats of formation ( ΔHorxn = - Q) that are close to zero. Therefore,the heat of formation of one component may be estimated if the heats of formation of the other components are known. In addition, ring strain in cycloalkanes and resonance stabilization in benzene may be computed.
| Reaction Conditions (RC) | Hyperhomodesmotic RC-5 |
Homodesmotic RC-4 |
Hypohomodesmotic RC-3 |
Isodesmic RC-2 |
Isogyric RC-1 |
|---|---|---|---|---|---|
1) Same number of CC bond types (CH3-CH2, CH3-CH ... etc.); 2) Same number of carbons (sp3, sp2, sp) with 0, 1, 2, 3 hydrogens. |
Yes | No | No | No | No |
1) Same number of CC bond types (sp3-sp3, sp3-sp2, sp3-sp, sp2-sp2, sp2-sp, sp2=sp2, sp2=sp, sp-sp ... etc.); 2) Same number of carbons (sp3, sp2, sp) with 0, 1, 2, 3 hydrogens. |
Yes | Yes | No | No | No |
1)Same number of carbon atoms in their various states of hybridization; 2) Same number of CH bonds, independent of hybridization, with 0, 1, 2, 3 hydrogens. |
Yes | Yes | Yes | No | No |
1) Same number of CC bonds of a given type: single, double, triple; 2) Same number of CH bonds. |
Yes | Yes | Yes | Yes | No |
1) Same number of carbons; 2) Same number of hydrogens. |
Yes | Yes | Yes | Yes | Yes |
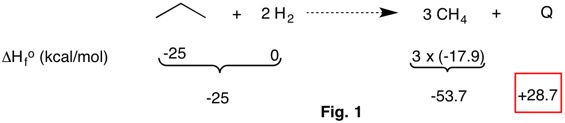
An isogyric reaction requires that the number of carbons and hydrogens in the reactants be equal to the number of carbons and hydrogens in the products. Clearly, this basic condition satisfies RC-2 in addition to RC-3, RC-4 and RC-5. Both sides of the reaction in Fig. 1 have three carbons and twelve hydrogens. A dotted arrow is drawn to indicate a possible hypothetical reaction. From the heats of formation of propane and methane the reaction becomes more negative and therefore exothermic. The value of Q = +28.7 kcal/mol indicates the amount of heat required to balance the heats of formation. Clearly, ΔHorxn = - Q. Why must this reaction be isogyric (RC-1) and not isodesmic (RC-2) or higher? In this instance, an isodesmic reaction requires two C-C single bonds among the products. There are only C-H bonds in methane. The reaction is isogyric!
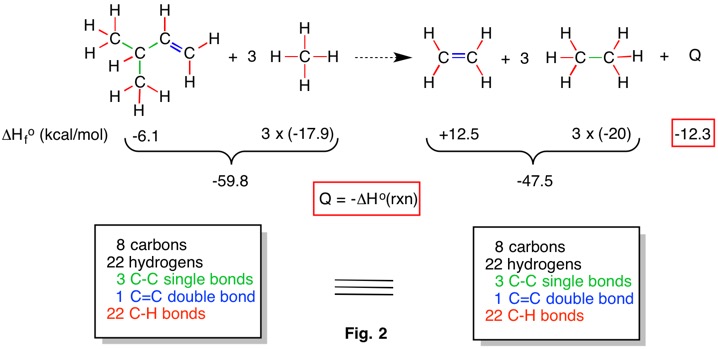
The reaction in Fig. 2 satisfies the requirements of an isogyric reaction in that both carbons and hydrogens are balanced on both sides of the equation. However, a more stringent requirement is met because there are three C-C single bonds, 1 C=C double bond and 22 C-H bonds for the reactants and products. There are 22 C-H bonds independent of the hybridization of the carbon atoms. No bond separation reaction containing methane can rise to the level of hypohomodesmotic because the latter category only permits a maximum of three C-H bonds per carbon.
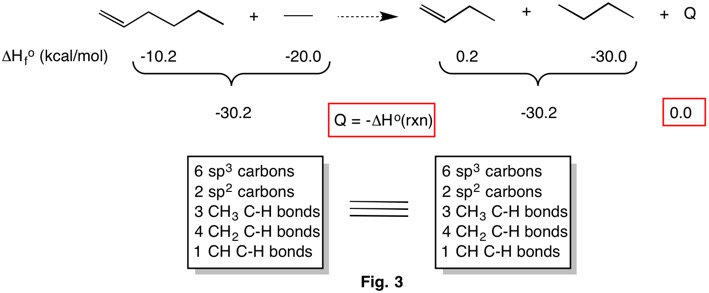
The hypohomodesmotic reaction (RC-3) takes into consideration the hybridization of carbon atoms. In Fig. 3 there are six sp3 and two sp2 hybridized carbons on each side of the reaction. Three carbons bear three hydrogens, four carbons bear two hydrogens and one carbon bears a single hydrogen on each side. There is no distinction as to the hybridization of carbon in counting C-H bonds. Whereas an isodesmic reaction can tolerate methane, the hypohomodesmotic reaction can only accommodate a maximum of three hydrogens per carbon. No bond separation reaction containing ethane can rise to the level of homodesmotic because the latter category does not permit a CH3-CH3 carbon-carbon bond on both sides of the reaction. The hypohomodesmotic reaction in Fig. 3 is also thermally neutral.
A homodesmotic reaction (RC-4) appears in Fig. 4. The carbon-carbon bonds are distinguished by the difference in hybridization of their carbon atoms. Unlike a hypohomodesmotic reaction (RC-3), the carbon-hydrogen bonds of a homodesmotic reaction are separated as a function of the hybridization of the carbon atoms. This latter distinction is more stringent than the requirement for C-H bonds under the RC-3 rubric. Unlike a hypodesmotic reaction, homodesmotic reactions classify C-H bonds as a function of the hybridization of the carbon atoms. There are the same number of hybridized bond types between reactants and products.

Fig. 6 is a hyperhomodesmotic (RC-5) version of the homodesmotic (RC-4) example in Fig. 4. The sp3-sp2 single bonds are separated into CH3-CH and CH3-C substitution patterns. Likewise, sp2=sp2 bonds are separated into three types: CH2=CH, CH2=C and CH=CH. The requirements for C-H bonds is the same as for homodesmotic reactions.
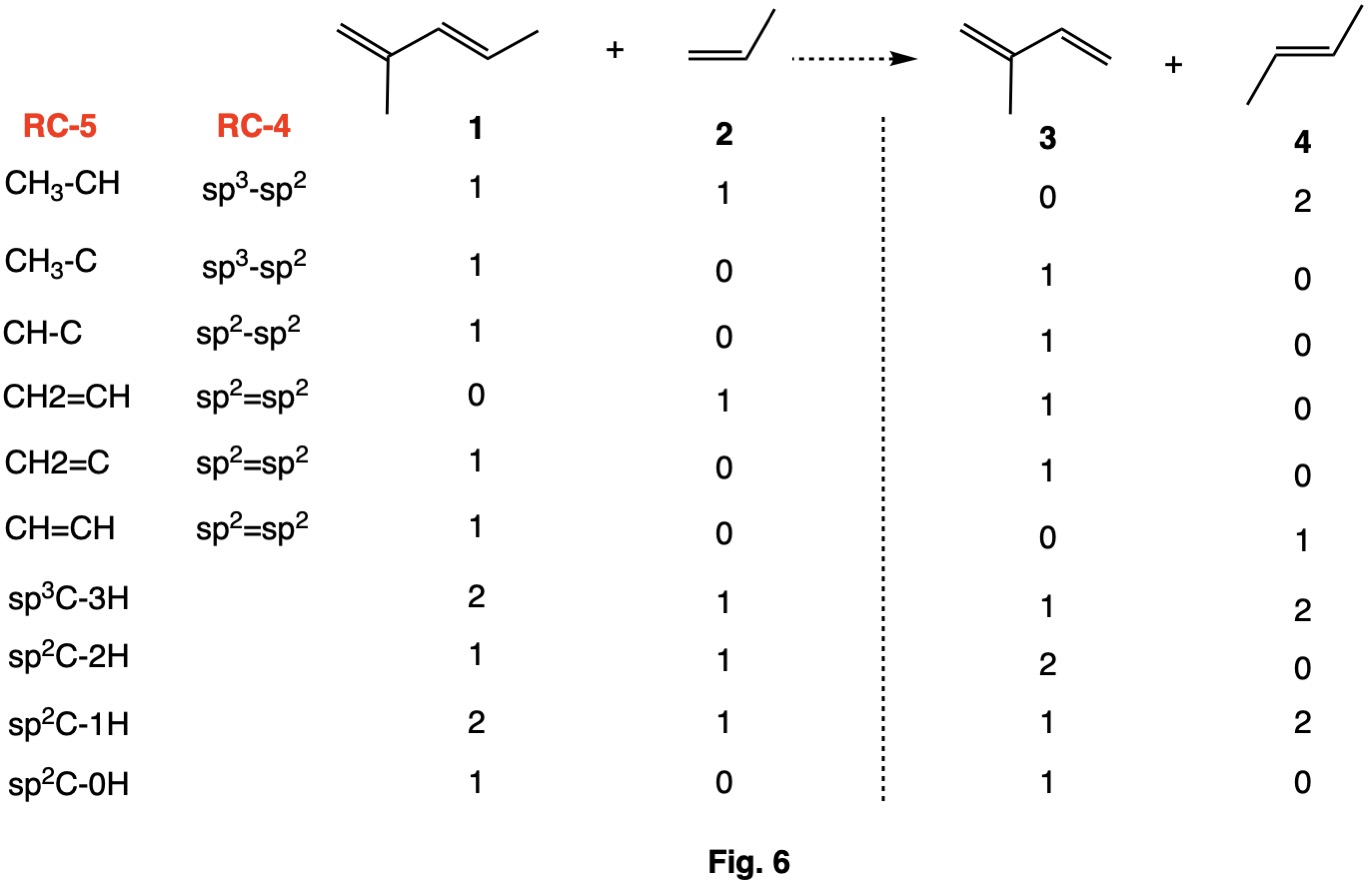
The heat of formation of (E)-2-methyl penta-1,3-diene is not listed in the NIST database. Assuming that this hyperhomodesmotic reaction is near thermoneutral (Fig. 6-1) and that the resonance contribution is similar in both dienes, the heat of formation is calculated to be +10.6 kcal/mol. Because the methyl groups in (E)-2-methyl-1,3-pentadiene are non-interacting and the double bond is not of the (Z)-configuration, the heat of formation can be determined by incrementally adding methyl groups to buta-1,3-diene (Fig. 6-2). Both (E)-penta-1,3-diene and 2-methyl buta-1,3-diene (isoprene) have heats of formation of +18.1 kcal/mol, a change of -8.2 kcal/mol per methyl group. The addition of a second, non-interacting methyl group would be expected to lower the heat of formation by another -8.2 kcal/mol giving a heat of formation of +9.9 kcal/mol, in close agreement with the solution in Fig. 6-1.
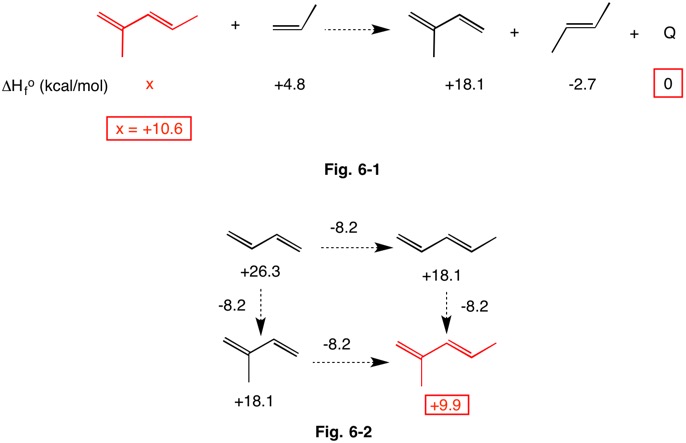
Fig. 7 is another example of a hyperhomodesmotic reaction. There are the same kinds of bonds on either side of the reaction. From the components known heats of reaction, the process is slightly endothermic. Assigning Q = 0, calculation of any one of the heats of formation from the known values of the other three, gives a result within 0.9 kcal/mol.
Strain Energy in Cycloalkanes:
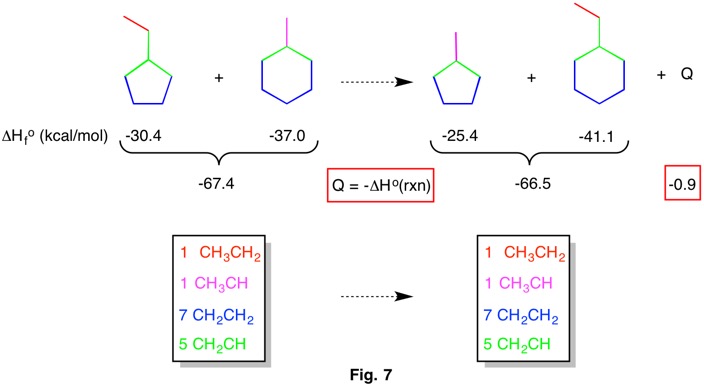
The hypohomodesmotic [8 sp3 carbons, 2 CH3 carbons and 6 CH2 carbons on each side of the reaction] examples of Fig. 8 provide a convenient method for computing the strain energy in simple cycloalkanes. The incremental methylene group in unstrained, normal alkanes is worth ~5 kcal/mol. In that cyclohexane is strain-free (-29.5 vs. -30 kcal/mol), the heat of the reaction (Q = -0.3 kcal/mol) is on the order of magnitude of the difference in the heat of formation of cyclohexane and the hypothetical value of -30 kcal/mol. Effectively, the value of Q is zero. Cyclopentane, cyclobutane and cyclopropane, unlike cyclohexane, all have strain energy, which is reflected in the value of Q. The strain energy of these three cycloalkanes determined by heat of combustion techniques are: cyclopentane, 6.5 kcal/mol; cyclobutane, 26.4 kcal/mol; cyclopropane, 27.6 kcal/mol. Clearly, there is good agreement between the two methods.

Resonance Stabilization of Benzene:
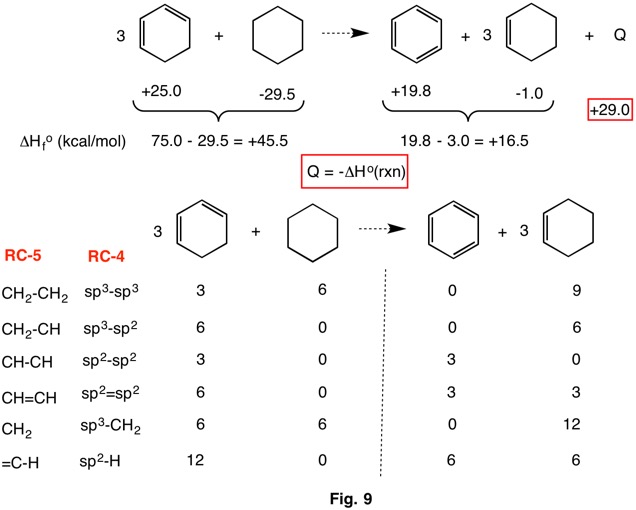
The resonance stabilization of benzene (Fig. 9) can be determined by a hyperhomodesmotic reaction because, as described in Fig. 7, the differently hybridized carbon-carbon bonds are each of a single type. There is correlation between bond types and hybridization on both sides of the equation. This calculation gives a value of -Q = -29.0 kcal/mol for the resonance stabilization of benzene .The usual resonance stabilization of benzene is taken as ~36 kcal/mol by comparing its heat of hydrogenation of the hypothetical "cyclohexatriene". This method is dependent on properly estimating the heat of hydrogenation of cyclohexatriene. Click here. This value is assumed to be three times the heat of hydrogenation of cyclohexene [3 x (|-29.5 + 1.0|) = 85.5 kcal/mol] to cyclohexane. [The heat of hydrogenation of benzene is -49.3 kcal/mol. The resonance stabilization of benzene would be 85.5 - 49.3 = 36.2 kcal/mol.] Because the heat of hydrogenation of 1,3-cyclohexadiene to cyclohexene is only 26 kcal/mol and the heat of hydrogenation of "cyclohexatriene" to 1,3-cyclohexadiene is unknown, the value of ~36 kcal/mol is probably an over estimation. For the resonance stabilization of benzene to have a value of 29.0 kcal/mol, the heat of hydrogenation of "cyclohexatriene" to 1,3-cyclohexadiene would have to be -23.8 kcal/mol.