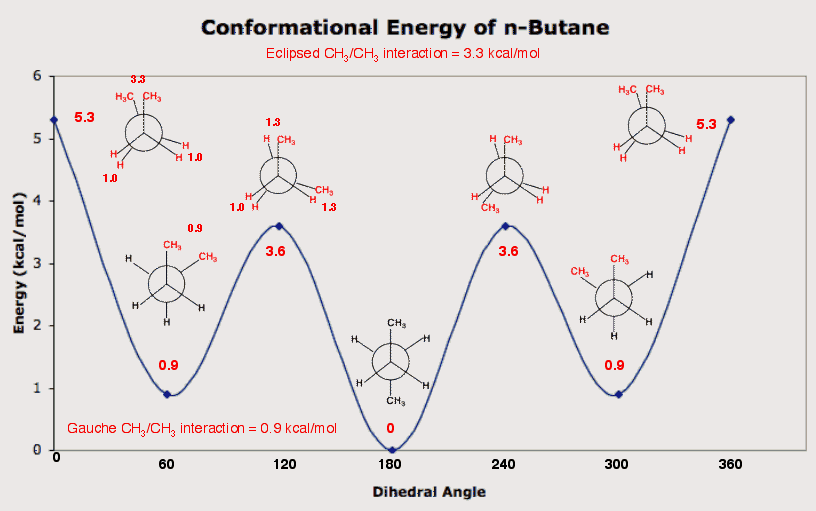
n-Butane is the smallest normal (straight chain) alkane that need not have all its carbon atoms in a plane. Ethane and propane must meet this condition. The best way to assess important steric interactions in n-butane is to examine rotation about the C₂-C₃ bond of n-butane. Consider the C₂-C₁ bond and the C₃-C₄ bond of n-butane as the hour and minute hands of a clock with the C₂-C₃ bond as the axis about which the hands of the clock pivot. If one hand is considered as fixed on the numeral twelve for the sake of reference, then six o'clock (C₁-C₂-C₃-C₄ dihedral angle = 180^o ) is represented by the anti conformation (staggered). Here C₁ and C₄, which may be considered as substituents on the C₂-C₃ bond, are as far apart from one another as possible. Also see that the three pairs of contiguous carbons, C₁-C₂, C₂-C₃ and C₃-C₄ are staggered. The C₁-methyl group bisects a H-C₃-H bond angle and the C₄-methyl group bisects a H-C₂-H bond angle. This arrangement is taken as 0 kcal/mol (cf., propane). One other all-staggered conformation is at two and ten o'clock. At dihedral angles of 60^o and 300^o (-60^o) the gauche (skewed) conformation is formed. This all-staggered (convince yourself) is higher in energy than the all-staggered anti conformation. The C₁-methyl group bisects the C₄-C₃-H bond angle and conversely the C₄-methyl group bisects the C₁-C₂-H bond angle. These arrangements are not separate interactions but a single one. The C₁- and C₄-methyl groups are close to one another and create torsional strain (C₁-C₂-C₃-C₄ dihedral angle = 60^o). The gauche conformation is 0.9 kcal/mol higher in energy than the anti conformation.

In addition to the two staggered conformations, anti and gauche, there are two eclipsed conformations. One is at noon (dihedral angle = 0^o) and the other is at four or eight o'clock (dihedral angle = 120^o and 240^o). The eclipsed conformations are formed by rotating the staggered conformations about the C₂-C₃ bond. In so doing, the C₂-C₃ substituents become eclipsed while the C₁-C₂ and C₃-C₄ substituents remain staggered. Confirm this statement for yourself. (In reality, all the C-C bonds and C-H bonds are rotating at all times. All permutations will not be considered.) Consider the 120^o eclipsed conformation. It has two pairs of CH₃-C/C-H bonds eclipsed and one C-H/C-H bond interaction. How many kcal/mol above the anti conformation does this eclipsed conformation lie? From ethane, a C-H/C-H eclipsed interaction was shown to be 1 kcal/mol. From propane, a CH₃-C/C-H eclipsed interaction was shown to be ~1.3 kcal/mol. Therefore, the 120^o eclipsed conformation of butane is 3.6 kcal/mol higher in energy than the anti conformation. In the 0^o eclipsed conformation there are two C-H/C-H and one CH₃-C/ CH₃-C eclipsed interactions. Given that this conformation is 5.3 kcal/mol higher in energy than the anti conformation, what is the approximate value of an eclipsed CH₃-C/ CH₃-C interaction? Each of the C-H/C-H eclipsed interactions is worth 1.0 kcal/mol. Thus by difference, the eclipsed CH₃-C/ CH₃-C interaction is worth 3.3 kcal/mol. Return to the Conformation Module.
.