Stereoisomers
Index:
Introduction:
During the first half of the 19th century organic chemistry was in a primitive state. Nothing was known of bonds as we understand them today. The structures of compounds were unknown and there were those individuals of the time who felt that nothing could be learned about structure--if indeed there was any. Chemists of the day were developing the skills to determine the composition of compounds by combustion analysis and gravimetric techniques. Invariably, if two different alkanes were found to contain different percentages of carbon and hydrogen, the physical properties of these substances --- melting point, boiling point, refractive index, etc. --- were different. They, indeed, were different!
On numerous occasions, compounds with different physical properties were found to have exactly the same elemental composition and molecular weight. Such compounds were called isomers, a term introduced by Berzelius in 1830. The term isomer is derived from Greek, meaning "equal parts".
Constitutional (structural) Isomers:
Constitutional isomers differ only in the connectivity of their atoms. The chart below shows the number of constitutional isomers possible for each of the acyclic alkanes CnH2n+2, where n=1-10. As the number of carbon atoms increases, the number of possible constitutional isomers increases rapidly.
|
|
|
The five constitutional isomers of the hexanes are illustrated in structures 1-5. Structure 1 can be rearranged to form the other four constitutional isomers. If you use an imaginary pair of "chemical scissors" to cut off a methyl group from the chain you will be left with a C1 and C5 fragment. You can reattach the C1 residue at C2 (the same as C4) of the C5 residue to form isomer 2, or add the C1 residue to C3 of the C5 fragment to obtain isomer 3. The remaining isomers 4 and 5, can be formed from two C1 units and a straight chain C4 fragment. All five hexane constitutional isomers have the same molecular formula, C6H14, and the same molecular weight, 86. However, each one of the hexanes has a unique boiling point.
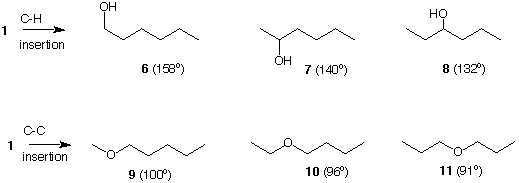
If once again we employ our "chemical scissors" to cut a unique C-H bond in n-hexane, structure 1, and insert a divalent oxygen at the point of scission, we will have formed three constitutionally isomeric hexanols: 1-hexanol (6), 2-hexanol (7) and 3-hexanol (8). Using the same technique to cut unique C-C bonds in n-hexane (1) followed by oxygen insertion, three ethers are formed: methyl n-pentyl ether (9), n-butyl ethyl ether (10) and di-n-propyl ether (11). Each of the six compounds has the molecular formula C6H14O, the same molecular weight, 102, but different boiling points. Note that the boiling points of the alcohols are uniformly higher than the boiling points of the ethers even though they all have the same mass. The higher boiling point of the alcohols is due to their ability to hydrogen bond, as does water which has a very high boiling point for its mass. A similar exercise could have been performed on hexanes 2-5 to produce a new series of alcohols and ethers.
Stereoisomers:
Stereoisomers are isomers that have the same atom connectivity but differ only in their orientation in space. Stereoisomers include geometrical isomers, diastereomers, and enantiomers. The most common definition of these three classes begins with enantiomers. Enantiomers are stereoisomers that are non-superimpoable mirror images of one another. Diastereomers are defined traditionally as stereoisomers that are not mirror images of one another. Geometrical isomers (cis-trans) are stereoisomers about a double bond. Rather than discuss the more complex stereoisomers first -- for indeed we have been progressing from the more complex isomers to the less complex ones -- we will consider enantiomers in the next section first, and then work our way toward the other stereoisomers -- diastereomers and geometrical isomers.
[Most textbooks use these definitions although the distinction between diastereomers and geometrical isomers arises because the definition implies that a diastereomer is chiral and a geometrical isomer is achiral. A simpler approach is to state that any pair of stereoisomers that are not enantiomers are diastereomers. Such a definition of a diastereomer removes the issue of chirality from the definition. Click here.]
Enantiomers:
Enantiomers are simply a pair of stereoisomers that are non-superimposable mirror images of one another. A substance must be chiral (handed), i.e., have no planes of symmetry or center of symmetry, to be an enantiomer. Enantiomers come in pairs only and they are not superimposable upon one another. A hand is the most common chiral entity. Your left hand mirrors your right hand and they are not superimposable on one another. Many common objects are chiral: screws, spiral staircases, gloves, shoes, most knots, etc. For an object to be achiral, it must have a minimum of one plane of symmetry. Some examples are: the human (external) body to a first approximation (bilateral symmetry), a coffee mug, a pair of reading glasses, etc.
Enantiomers are most commonly formed when a carbon atom (sp3 hybridized) contains four different substituents. There are two ways to attach the substituents to the quadrivalent carbon. The two arrangements are enantiomers of one another. The carbon atom in such species is often said to be chiral but this is a misnomer. It is not the carbon atom that is chiral but rather the environment around the carbon atom. The property of chirality, as we have seen, is independent of chemistry and, for that matter, atoms. In the enantiomers 12 and 13 shown below (How to manipulate JSmol structures), imagine that the black "ball" is totally invisible against the black background. The four colored balls form a chiral environment independent of the black ball and the "sticks" that keep the four colored balls spaced apart.
[An important corollary of this example is that the union of an achiral entity with a chiral entity results in a chiral entity. A ball (achiral) in a hand (chiral) is chiral.]
-12-
-13-
-14-
-15-
If the color of any one of the colored balls is changed to one of the other three colors, (14, in this case two red balls), a plane of symmetry will arise and thus the arrangement of balls will be achiral, and the arrangement of balls will be superimposable on its mirror image. In an achiral entity, or molecule, that contains one plane of symmetry (determined by the plane of the green, yellow and black balls), the plane of symmetry serves as a mirror that reflects both halves of the object, each half being chiral. This situation is the same as placing your left hand against your righthand, fingertip-to-fingertip, palm-to-palm, to form an achiral pair of hands. [If you interlock your fingers with the left thumb closer to you, the pair of hands is chiral. Its mirror image is formed by interlocking your fingers with the right thumb closer to you.] Arrangement 15 has two planes of symmetry. In this case, the "lefthand" side of either given plane is superimposable on its "righthand" side.
|
In summary, the most common source of chirality in organic chemistry is the "asymmetric carbon", or, better yet, the carbon at a center of asymmetry. We showed that the carbon only serves the capacity of keeping the four different atoms, or colored balls if you wish, where they belong. But an asymmetric carbon is not the only source of chirality. Conformations of molecules, and molecules themselves, can be chiral without having an asymmetric carbon. Consider the gauche conformations 16 and 17 of n-butane as an example of a chiral molecular conformation. [If you need a refresher on this topic, click here.] n-Butane has no asymmetric carbons but yet the two gauche conformations are mirror images of one another, equal in energy and present in equal amounts. These two conformations constitute a racemate whose enantiomers are rapidly interconverting by rotation about the C2-C3 sp3 hybridized bond. The formation of enantiomers by bond rotation in achiral molecules is called stochastic (random) chirality [Mislow]. At ambient temperaturethey cannot be separated. The net racemic gauche conformation and the achiral anti conformation are the major conformations of n-butane, which of course is optically inactive. Gauche butane defines a screw axis, one conformation is left-handed and the other is right-handed. |
-16-
-17-
|
|
A similar situation exists in the class of compounds known as allenes, RHC=C=CRH. 1,3-Disubstituted allenes can exist as racemates that can be separated (resolved) into their enantiomers. Structures 18 and 19 are the two enantiomers of 1,3-dimethylallene. Although they define a screw axis, the sp hybridized central carbon prohibits rotation about the central, linear carbon axis (C2-C4). There is no asymmetric carbon to be seen in these structures.
|
Diastereomers:
-20a-
-20b- |
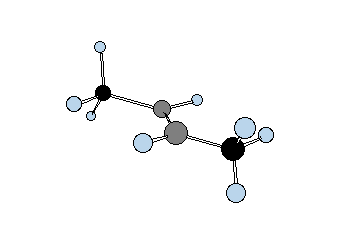
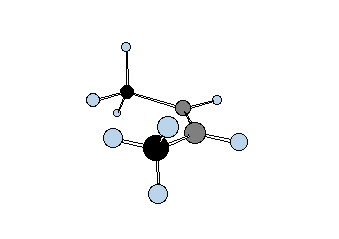
Diastereomers are stereoisomers that are not enantiomers. How is this possible? Consider two gray tetrahedral "asymmetric carbons" that are bonded to each other and each one has three atoms attached: red, yellow and green. Structures 20a and 21a represent one staggered conformation of both possible arrangements. Each one is clearly a stereoisomer of the other because they both have the same atom connectivity. Rotation about the C-C bond of staggered conformation 20a, which is a chiral representation, by 60o gives eclipsed conformation 20b, which clearly is achiral. A mirror plane can be passed through the C-C bond. |
-21a-
-21b-
|
Another 60o rotation of the eclipsed conformation 20b in the same direction produces the enantiomer (mirror image) of 20a,---namely, ent-20a. This is another example of stochastic chirality that was encountered above in the discussion of n-butane. Achiral structure 20 is called a meso compound. It cannot be separated into enantiomers because it is achiral and its mirror image is necessarily superimposable on itself. On the other hand, the diastereomer of 20 -- namely 21 -- is chiral. In either the staggered conformation 21a or the eclipsed conformation 21b, or in any conformation you wish to make, there is no mirror plane.
Diastereomer 21 is chiral no matter how much bond rotation
occurs. This means that 21 is a diastereomer of 20 and
structure 21 must have an
enantiomer,
ent-21.
Diastereomer 21 and its enantiomer form a racemate called a
d,l-pair. Each enantiomer of a d,l-pair is chiral and the
racemate is capable, in principle, of resolution into its
enantiomers.
Now imagine converting one of the red atoms in 20 and 21 to violet as shown in 22 and 23, respectively. In so doing the possibility of a meso isomer has been removed. Any one structure is a diastereomer of two others and an enantiomer of one. Convince yourself of these diastereomeric and enantiomeric relationships by manipulating the structures.
|
-22-
|
|
-23- |
|
|
|
|
|
-ent-22-
|
|
-ent-23-
|
Geometrical Isomers:
Geometrical isomers (E/Z-isomers) are stereoisomers about double bonds. They are achiral. (E)-2-Butene (left below) and (Z)-2-butene (right below) are both achiral and both isomers are superimposable on their mirror respective mirror images. They are each distinct alkenes with unique properties and they are not (readily) interconverted. Rotation about the strong double bond (gray atoms) is prohibited.