Optical Rotation Calculations

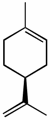
(S)-limonene [α]D -94o

The two enantiomers of limonene occur in nature. Ideally, the two enantiomers should have specific rotations that are opposite in sign and equal in magnitude. Either sample might be contaminated with impurities that either raise the rotation or lower it. Additionally, errors in weighing samples may contribute to a difference in absolute value of the rotation. Assuming that the (S)-enantiomer is contaminated with the (R)-enantiomer and that the latter enantiomer is pure, how does one compute the percentage of each enantiomer?

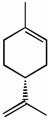
(R)-limonene [α]D +115o

Part A:

The value of -94^o for the (S)-enantiomer is [α]_obs. Thus,

[α]_obs = [rotation (R)][n_R] + [rotation(S)][n_S] where rotation (R) = - rotation (S) and n_R + n_S = 1 (n = mole fraction)

Therefore,

[α]_obs = [rotation (R)][n_R] - [rotation(R)][1-n_R]

Rearranging,

[α]_obs = [rotation (R)][2n_R - 1] or [2n_R - 1]= [α]_obs/[rotation (R)]

The term [2n_R - 1] is the fractional optical purity (op) or enantiomeric excess (ee). When n_R = 1, the observed rotation is the rotation of (R). If n_R = 0, the observed rotation is that of the pure (S) enantiomer. When n_R or n_S = 0.5, the observed rotation is zero; the sample is racemic. To convert this equation to percent: op = ee = 100x[α]_obs/[rotation (R)]

Because the (S)-enantiomer of limonene has a negative value, the major component must be levorotatory. Substituting S for R, op = [α]_obs/[rotation (S)] = -94/-115 =0.82.

Therefore,

op = 0.82 = [2n_S- 1] or n_S = 1.82/2 = 0.91; n_R = 0.9.

The (S)-limonene is 91% (S)-enantiomer and 9% (R)-enantiomer.

Part B:

Since op = ee = 100x[α]_obs/[rotation (R)] = |R - S|/(R + S), it is possible to find the percentages of R and S algebraically. One is looking for two numbers whose absolute difference is |R - S| = 82 and whose sum is R + S = 100. Adding these two equations and knowing that the (S)-enantiomer is in excess, we have 2S = 182; S = 91% and R = 9%.