The Gay-Lussac Method of Vapor Density Measurement

Measurement of the Weights of Vapors at a Given Volume and at Determined Pressure and Temperature. J. B. Biot, Traite de Physique Experimentale et Mathematique Vol. I, pg. 291, (1816) (translated by Amelie Berube) From the experiments reported in the previous chapter we were able to determine that a very small amount of liquid was sufficient to give a considerable volume of vapor. Several physical and chemical studies required the knowledge of the volume of this expansion; in other words, that we could determine the volume of vapor that could be given by a given weight or by a given volume of each liquid. But, this determination seemed quite difficult because the expansion of the vapor was substantial. Unfortunately, it was not possible to recondense in one mass the liquid used to generate it. Fortunately, M. Gay-Lussac eluded this difficulty by reversing it, in other word, by determining the volume of vapor that can be produced by a given volume of liquid. you first have to determine the exact volume of liquid used, which is the real difficuly. M. Gay-Lussac blows small glass bubbles (BB, Fig. 83) [Note: Fig. 83 nor the bubbles B were designated in Appendix III. They appear in the upper righthand corner of Fig. 84 to the right.] They are nearly spherical , but one side has an elongated spout. We first weigh one of the little

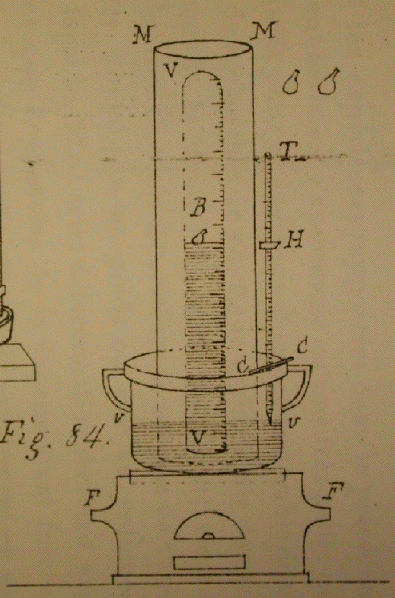
Appendix III

bubbles when it is filled with air; we then introduce the liquid the same way we would for a thermometer by emerging it in the liquid after warming it up to release most of the air. When the small bubble is mostly full, the spout is sealed with a torch. This procedure does not change the composition of the glass but simply the shape of the bubble. We then weigh the filled bubble again and by subtracting the weight of the glass shell previously weighed, we obtain the weight of the liquid that it contains. We will soon see how we can deduce its volume. To now transform all this liquid into vapor, M. Gay-Lussac uses an apparatus similar to the one M. Dalton used to observe the tension of vapors under vacuum. He uses a long narrow glass dome (VV, Fig. 84)., which is divided in sections of equal volume and the total volume is about 1.5 liters. He fills it with mercury and puts it upside-down and then he introduces the small bubble filled with liquid (B). The bubble reaches the top of the tube. We now vaporize it. To do so, M. Gay-Lussac covers the dome with a glass envelope (MM) longer than the tube so its lower portion is plunged into the mercury. He fills the cylinder with water and the dome is then covered. The apparatus is placed on on a stove (FF) and a fire is lighted up. as the water and mercury are warmed, the liquid in the bubble is also warmmed. The liquid in the the bubble expands and breaks the glass shell, spreads at the top of the dome and soon becomes vapor. The temperature is increased until the water in the cylinder is boiling. [Note: Water is applicable for liquids that boil below 100 oC.] We then measure the height of the mercury column that remains in the dome above the exterior level. this is how m. Gay-Lussac operates to be as accurate as possible. The sides of the shallow basin (vv) are made of cast-iron are straight and leveled horizontally. He sets on the side a ruler made of copper (cc) with a garaduated rod (T) set vertically so its tip barely touches the surface of the mercury outside. A marker (H) that goes up and down along the vertical rod is set at the same level as the mercury inside the dome. The elevation of mercury can the be measured precisely. The difference (between the height of the mercury column and the atmospheric pressure measured in the same units) represents the elastic force of the vapor contained in the dome. In other words, the pressure that it sustains. We know the volume of this vapor by the number of sections that it occupies in the dome. With these values we can calculate the ratios of volumes for the liquid and the vapor at a given temperature and pressure.